Zapis koordinat v sistemu UTM
O koordinatnih sistemih in pretvarjanju med različnimi zapisi koordinat GPS smo že pisali. Ponovimo na kratko. Geografska širina in dolžina izbrane točke na Zemljini površini sta v resnici dva kota. Prvi je kot med ekvatorialno ravnino in zveznico med točko in centrom Zemlje, drugi pa kot med ničelnim poldnevnikom in poldnevnikom skozi točko. Kota, ki ju imenujemo tudi koordinati, podamo v stopinjah ter njihovih manjših razdelkih, iz česar dobimo različne zapise koordinat (na primer decimalne stopinje, stopinje s kotnimi decimalnimi minutami, stopinje s kotnimi minutami in sekundami).
Omenjeni koordinatni sistem z dvema kotoma je naraven za opis površine krogle. V vsakdanjem življenju ukrivljenosti planeta niti ne opazimo (zaradi česar še danes nekateri verjamejo v ploščato Zemljo), na ravnini pa je bolj naraven pravokotni koordinatni sistem s koordinatami v metrih. Pretvorba iz tisočink kotnih minut ali kotnih sekund v metre ni enolična, saj je odvisna od naše lokacije, o čemer smo tudi že pisali. Da je nemogoče krogelno površino sploščiti brez deformacije ve vsak, ki je že kdaj skušal izravnati pomarančni olupek ali prebodeno žogo. Gre le, če je kos olupka dovolj majhen, potem se že sam po sebi zdi ploščat. Podobno lahko lokalno majhen del sicer okrogle površine upodobimo kot ravnino brez večjih popačenj. Ker s seboj ne nosimo globusa, zemljevidi in zasloni telefonov pa so ploščati, smo praktično prisiljeni uporabljati projekcijo sfere na ravnino.
Univerzalna Transverzalna Merkatorjeva projekcija
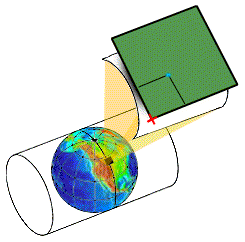
Merkatorjeva projekcija (prvi jo je uporabil slavni kartograf Gerardus Mercator v 16. stoletju) je valjna kartografska projekcija, pri kateri so vzporedniki in poldnevniki ravne linije, ki se sekajo pod pravim kotom. Sliko dobimo tako, da kroglo ovijemo v valj, preslikamo detajle s krogle na valj in valj razgrnemo. Nepopačen je seveda samo del na dotikajočem se poldnevniku, z oddaljenostjo od njega popačenje raste. Če vzamemo valj z malce manjšim premerom od krogelnega, tak valj kroglo seka v dveh poldnevnikih, potem so detajli na obeh poldnevnikih točni. Izkaže se, da je povprečno popačenje take projekcije manjše in se jo danes pogosteje uporablja.
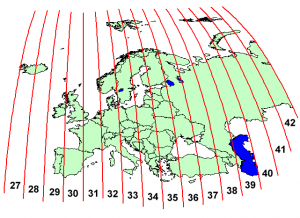
Na njej temelji zapis koordinat UTM (Universal Transverse Mercator), ki ga lahko zasledimo na centralnem geolovskem spletišču pri opisu vsakega zaklada, pa tudi v kakšni prebrisani uganki. V tem sistemu Zemljo podobno kot pomarančo razrežemo na 60 con po poldnevnikih, kapici okoli severnega in južnega pola (pod 80° južno in nad 84° severno) pa odrežemo proč. Hitro izračunamo, da vsaka cona zavzame 360°/60 = 6° zemljepisne širine. Vsak tak trak je najširši na ekvatorju, in sicer približno 40000km/60 = 667km. Cone oštevilčimo tako, da začnemo pri datumski meji (zemljepisna dolžina 180° zahodno in nadaljujemo proti vzhodu). Pri ničelnem (Greenwichevem) poldnevniku se stikata coni 30 in 31. Oštevilčenje se nadaljuje proti vzhodu, kjer je zadnja cona številka 60, ki se dotakne cone 1. Slovenija cela pade v cono 33, ki pokriva med 12° in 18° vzhodne dolžine. Skoraj vse cone so enake oblike, nekje so jih po dogovoru malce prikrojili geopolitičnim razmeram (npr. okoli Norveške). Beseda transverzalna pomeni le, da je projekcijski valj ležeč in se Zemlje dotika v poldnevniku, v nasprotju z “navadno” Mercatorjevo projekcijo, kjer je ta valj pokončen in se Zemlje dotika po ekvatorju.
Koordinate v smeri zahod-vzhod (E) merimo v metrih in sicer kar kot oddaljenost od središčnega poldnevnika posamezne cone proti vzhodu. V coni 33 je ta središčni poldnevnik 15° (na sredini med 12°in 18°). Da pa ne uvajamo pozitivnih in negativnih številk, razdalji prištejemo 500km. Tako imajo vse točke na centralnem poldnevniku vsake cone vzhodno koordinato 500000. Tiste, ki so 10 kilometrov proti zahodu imajo koordinato 490000, tiste, ki so 20km proti vzhodu imajo koordinato 520000 itd. Ne pozabimo, koordinate so izražene v metrih!
Koordinate v smeri jug-sever (N) merimo kot oddaljenost od ekvatorja v metrih proti severu. Na severni polobli to pomeni številke približno med 0 in 9300000. Ker ne želimo negativnih števil, na južni polobli prištejemo 10000km. To pomeni, da ima ekvator severno koordinato 10000000, proti jugu pa se številke zmanjšujejo.
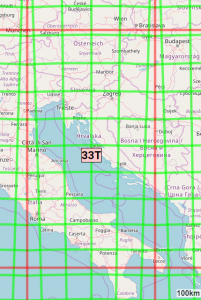
Samo koordinate N in E v zapisu UTM ne zadostujejo, saj se identične koordinate pojavijo v vsaki od 60 con. Večina celo dvakrat v coni, enkrat severno in enkrat južno od ekvatorja. Zato moramo pri navajanju koordinat UTM obvezno navesti cono in pa, ali gre za severno ali južno poloblo. Pri razvoju sistema UTM so posamezno cono razdelili na dele še v smeri jug-sever in sicer na 20 podcon (večinoma po 8°) od juga proti severu. Označili so jih s črkami od C do X brez I in O (da ne pride do zamenjave s številkama 1 in 0). Slovenija leži cela v podconi T, tako da je celotno ime naše cone 33T. Podcona tudi jasno pove, ali so koordinate severno ali južno od ekvatorja, druge uporabne vrednosti, razen grobega lociranja, pa črka podcone nima. Črka N in njej sledeče vse ležijo na severni polobli, tiste pred N pa na južni.
Oštevilčenje con (spodnja vrstica) in podcon (stolpec skrajno desno). Na severu Evrope opazimo, da imajo nekatere cone po dogovoru drugačne velikosti kot večina.
Kako zapišemo koordinato v UTM?
1. Navedemo cono in podcono
2. Navedemo koordinato v smeri E (v metrih)
3. Navedemo koordinato v smeri N (v metrih)
Črk “E” in “N” načeloma ni potrebno navajati, lahko pa jih. Včasih so navedene pred ustrezno številko, včasih pa za njo. Občasno srečamo tudi “mE” in “mN”, kar beremo kot “metrov vzhodno” in “metrov severno”.
Primer: 33T 457966 5106809
Točka je v naši coni (33T), od centralnega poldnevnika (15°) je oddaljena 500000-457966 = 42034 metrov proti zahodu, od ekvatorja pa 5106809 metrov (proti severu, seveda). Je ob kandelabru.
Naštejmo nekaj prednosti zapisa položaja v UTM:
- kvadratna mreža v metrih,
- desetiški sistem, nobenih stopinj, kotnih minut, pretvornika 60,
- ni negativnih vrednosti, nobenih oznak za stopinje, minute, sekunde, zapis je sestavljen zgolj iz črk in številk, primeren za radijsko komunikacijo, morzejevo kodiranje in podobno,
- številke naraščajo proti severu in proti vzhodu, to je gor in v desno, tako kot pri kartezičnem koordinatenm sistemu X-Y, ki ga učijo v šoli. Velja enostavna kartezična matematika (razdalje, premice, sekanja), sferna trigonometrija ni potrebna. Znotraj posamezne cone je napaka v razdaljah pod 1/1000.
Sistem UTM je torej dober lokalni približek ploščate Zemlje.
Primer izračuna razdalje
Po udeležbi na šmarnogorskem dogodku je Peter končno izpolnil pogoje in postal eventofrik. Neučakan kakor je, je želel s hriba poleteti s padalom direktno do zaklada z izzivom. Za oceno težavnosti tega podviga je potreboval razdaljo med obema točkama.
Šmarna gora:
N 46° 07.803 E 014° 27.808
UTM: 33T E 458552 N 5108637
Eventofrik:
N 45° 58.830 E 014° 34.273
UTM: 33T E 466786 N 5091970
Račun s sferno trigonometrijo bi dal razdaljo 18597m. A glej ga zlomka, baterija v Petrovem telefonu je bila prazna. Na voljo je imel le starejši kalkulator, s katerim je bližnji gostilničar pred uvedbo davčnih blagajn sešteval dnevni izkupiček. Spomnil se je Pitagorovega izreka in izračunal kvadrat hipotenuze: (458552–466786)^2 + (5108637–5091970)^2 = 345587645, ko je to številko korenil, je dobil oddaljenost 18590m, kar je vsega 7m razlike glede na sferični račun. Zgodba sicer ne govori, ali se je Peter ob tem rezultatu odločil skočiti in kako se je avantura končala, morda bo kaj o tem zapisal v dnevnik.
Vojaški zapis (MGRS)
Uporabnosti zapisa UTM je prepoznala tudi vojska. Z nekaj modifikacijami je postal standard NATA, imenuje se MGRS (za Military Grid Reference System). Avtor teh vrstic je zapis MGRS že nekajkrat zasledil v zakladih z uganko, zato ga je vredno omeniti.
Zapis cone in podcone je popolnoma enak kot pri UTM, za nas torej 33T. Cono še dodatno razdelijo na kvadrate s stranico 100km in jih označijo z dvema črkama AA, AB,… Sledita koordinati glede na ta 100km velik kvadrat, pri čemer si lahko izberemo natančnost navajanja. Za največjo (metrsko) natančnost, povemo 5 cifer, torej med 00000 in 99999. Za natančnost 10 metrov zadostujejo 4 cifre, za kilometrsko pa le 2 cifri pri vsaki koordinati. Koordinati si sledita kot pri UTM, najprej E, potem N, vse številke zlepimo skupaj.
Tako je na primer Šmarna gora v 33TVM5808 (1km kvadrat), cerkev in igrišče v 33TVM585086, miza s kavo pa na 33TVM58550865.
Marsikdo bi iz zgoraj povedanega zaključil, da je zapis UTM bolj praktičen kot kotni zapis, ki smo ga navajeni, saj se naša aktivnost dogaja na majhnem področju, ki ga UTM dobro opiše. Zakaj ni bolj v uporabi med geolovci? Osebno sicer ne poznam nobenega geolovca, ki bi redno uporabljal ta sistem in ga imel vključenega na GPSu. Je kdo tak? Komentarji dobrodošli.







Super članek! Splošno sem UTM poznal, nisem pa se nikoli spuščal v detajle. Zdaj mi je jasno, kaj pomeni T v UTM. Zanimiva je tudi razdelitev MGRS za severni in južni pol – glej wiki link slike.
Pozdravljeni,
Eno praktično vprašanje. Geodetska uprava RS mi je poslala podatke o centroidu, na primer E 442680,43 N 43250,44. Na GPS-u, ko kliknem na to lokacijo, dobim natančno vrednost E, ne pa tudi vrednosti N. Vrednost N mi pokaže 50245.34 Približno.
Ali gre za napako na strani GURS-a ali gre za drugo funkcijo?
Še eno vprašanje v istem kontekstu. Ko poskušam pretvoriti podatke Centroid v UTM, sploh ne morem vnesti kode 33T, vedno mi vrne 33N, zato ne morem dobiti natančne lokacije v Sloveniji. Ali mi lahko kdo pomaga dobiti koordinate parcele na zemljevidu? Hvala za kakršno koli pomoč. Lp Benjamin